Abstract
Dijkstra's Algorithm is one of the most popular algorithms in computer science. It is also popular in operations research. It has many attractions for both lecturers and students. Unfortunately, however, a number of important features of this fascinating algorithm are not as transparent to the average user as they should be. In particular, one of the consequences of the history of the algorithm is that it is generally regarded as a computer science method rather than as an operations research method. This is a pity!
In this paper we attempt to change this perception by providing an OR/MS perspective on the algorithm. In particular, we are reminded that this famous algorithm was strongly inspired by Bellman's Principle of Optimality and that both conceptually and technically it constitutes a dynamic programming successive approximation procedure par excellence. One of the immediate implications of this perspective is that this popular algorithm can be incorporated in the dynamic programming syllabus and in turn dynamic programming must be (at least) alluded to in a proper exposition/teaching of the algorithm.
Educationally oriented interactive modules are provided for experimentation with this intriguing and powerful algorithm.
In 1959 a three pages long paper entitled A Note on Two Problems in Connexion with Graphs was published in the journal Numerische Mathematik. In this paper Edsger W. Dijkstra - then a twenty-nine-year-old computer scientist - proposed algorithms for the solution of two fundamental graph theoretic problems: the minimum weight spanning tree problem and the shortest path problem. We shall say a bit more about this paper later on in this discussion. For the time being suffice it to say that today Dijkstra's Algorithm for the shortest path problem is one of the most celebrated algorithms in computer science (CS) and a very popular algorithm in operations research (OR).
In the literature this algorithm is often described as a greedy algorithm. For example, the book Algorithmics (Brassard and Bratley [1988, pp. 87-92]) discusses it in the chapter entitled Greedy Algorithms. The Encyclopedia of Operations Research and Management Science (Gass and Harris [1996, pp. 166-167]) describes it as a "... node labelling greedy algorithm ... " and a greedy algorithm is described as "... a heuristic algorithm that at every step selects the best choice available at that step without regard to future consequences ..." (Gass and Harris [1996, p. 264]).
Although the algorithm is very popular in the OR/MS literature, it is generally regarded as a "computer science method". Apparently this is due to three factors: (a) its inventor was a computer scientist (b) its association with special data structures, and (c) there are competing OR/MS oriented algorithms for the shortest path problem. It is not surprising therefore that some well established OR/MS textbooks do not even mention this algorithm in their discussions on the shortest path problem (eg. Daellenbach et al [1983], Hillier and Lieberman [1990]) and those that do discuss it in that context present it in a stand-alone mode, that is, they do not relate it to standard OR/MS methods (eg. Markland and Sweigart [1987], Winston [2004]). For the same reason it is not surprising that the "Dijkstra's Algorithm" entry in the Encyclopedia of Operations Research and Management Science (Gass and Harris [1996, pp. 166-167]) does not have any reference whatsoever to dynamic programming.
The objective of this paper is to present a completely different portrayal of Dijkstra's Algorithm, its origin, its role in OR/MS and CS, and its relationship to other OR/MS methods and techniques. Instead of focusing on its computational complexity, data structures that it can utilize to good effect, and other implementation issues, we examine the fundamental principle that inspired it in the first place, its basic structure, and its relationship to well established OR/MS methods and techniques. That is, we show that at the outset Dijkstra's Algorithm was inspired by Bellman's Principle of Optimality and that, not surprisingly, technically it should be viewed as a dynamic programming successive approximation procedure.
Be it as it may, one of the immediate implications of this fact is that OR/MS lecturers can present Dijkstra's Algorithm as an OR/MS-oriented algorithm par excellence and relate it to well established OR/MS methods and techniques. In particular, they can incorporate Dijkstra's Algorithm in the dynamic programming syllabus where in fact it belongs. This, we should add, is long overdue for in teaching Dijkstra's Algorithm it is most constructive to draw the students' attention to the fact that this algorithm was inspired by Bellman's Principle of Optimality. Furthermore, it is important to point out that it is no more, no less than a (clever) method for solving the dynamic programming functional equation for the shortest path problem given that the arc lengths are nonnegative.
The basic facts about the intimate relationship existing between Dijkstra's Algorithm and dynamic programming are definitely well documented in the specialized literature (eg. Lawler [1976] and Denardo [2003]) but are not accessible to the majority of students whose first encounter with dynamic programming and/or Dijkstra's Algorithm is via general purpose introductory courses in OR/MS and/or CS. This paper is written very much with these students - more precisely their lecturers - in mind.
In short, our analysis aims at giving Dijkstra's Algorithm an OR/MS perspective by focusing on its relationship with standard dynamic programming methods and techniques. This, we hope, will contribute to a fuller understanding of both by lecturers and students alike. Our primary target audience consists then of two - not necessarily mutually disjoint - groups: Lecturers teaching dynamic programming and/or Dijkstra's Algorithm as topics in specialized subjects and/or in much broader OR/MS and CS subjects.
In the next section we describe the basic structure of the classical shortest path problem and then briefly examine this problem from an algorithmic point of view by referring to two popular classes of OR/MS algorithms. One is inspired by linear programming, the other by dynamic programming formulations of the shortest path problem. We then describe Dijkstra's Algorithm and identify the class of shortest path problems it was designed to solve. Finally we discuss the relation between Dijkstra's Algorithm and dynamic programming.
It is interesting to note that despite the popularity of the algorithm, in fact perhaps precisely because of it, over the years its literature has generated not only useful results but also misinterpretations, misrepresentations and plain errors. It is therefore important to deal with this issue - at least mention it - in the classroom and in textbooks. We briefly discuss this matter under the heading Temptations.
For the benefit of lecturers who are teaching dynamic programming, we provide two appendices. One provides a dynamic programming perspective on Dijkstra's Algorithm and one gives a brief overview of the generic successive approximation method.
Regarding style of presentation: we deliberately adopt a semi-formal approach. It must be stressed therefore that our discussion is readily amenable to a much less formal exposition and interpretation, as well as to a much more formal and rigorous technical treatment.
A number of educationally oriented interactive modules are provided for experimentation with Dijkstra's Algorithm and related ideas.
One of the main reasons for the popularity of Dijkstra's Algorithm is that it is one of the most important and useful algorithms available for generating (exact) optimal solutions to a large class of shortest path problems. The point being that this class of problems is extremely important theoretically, practically, as well as educationally.
Indeed, it is safe to say that the shortest path problem is one of the most important generic problems in such fields as OR/MS, CS and artificial intelligence (AI). One of the reasons for this is that essentially any combinatorial optimization problem can be formulated as a shortest path problem. Thus, this class of problems is extremely large and includes numerous practical problems that have nothing to do with actual ("genuine") shortest path problems.
New classes of genuine shortest path problem are becoming very important these days in connection with practical applications of Geographic Information Systems (GIS) such as on line computing of driving directions. It is not surprising therefore that, for example, Microsoft has a research project on algorithms for shortest path problems.
What may surprise a bit our students is how late in the history of applied mathematics this generic problem became the topic of extensive research work that ultimately produced efficient solution methods. However, in many respects it is not an accident at all that this generic problem is so intimately connected to the early days of OR/MS and electronic computers. The following quote is very indicative (Moore [1959, p. 292]):
The problem was first solved in connection with Claude Shannon's maze-solving machine. When this machine was used with a maze which had more than one solution, a visitor asked why it had not built to always find the shortest path. Shannon and I each attempted to find economical methods of doing this by machine. He found several methods suitable for analog computation, and I obtained these algorithms. Months later the applicability of these ideas to practical problems in communication and transportation systems was suggested. |
For the purposes of our discussion it is sufficient to consider only the "classical" version of the generic shortest path problem. There are many others.
Consider then the problem consisting of n > 1 cities {1,2,...,n} and a matrix D representing the length of the direct links between the cities, so that D(i,j) denotes the length of the direct link connecting city i to city j. This means that there is at most one direct link between any pair of cities. The distances are not assumed to be symmetric, so D(i,j) is not necessarily equal to D(j,i). The objective is to find the shortest path from a given city h, called home, to a given city d, called destination. The length of a path is assumed to be equal to the sum of the lengths of the links between consecutive cities on the path. With no loss of generality we assume that h=1 and d=n. So the basic question is: what is the shortest path from city 1 to city n?
To be able to cope easily with situations where the problem is not feasible (there is no path from city 1 to city n) we deploy the convention that if there is no direct link from city i to city j then D(i,j) is equal to infinity. Accordingly, should we conclude that the length of the shortest path from node i to node j is equal to infinity, the implication would be that there is no (feasible) path from node i to node j.
Observe that subject to these conventions, an instance of the shortest path problem is uniquely specified by its distance matrix D. Thus, this matrix can be regarded as a complete model of the problem.
As far as optimal solutions (paths) are concerned, we have to distinguish between three basic situations:
- An optimal solution exists.
- No optimal solution exits because there are no feasible solutions.
- No optimal solution exists because the length of feasible paths from city 1 to city n is unbounded from below.
Ideally then, algorithms designed for the solution of shortest path problems should be capable of handling these three cases.
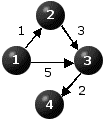
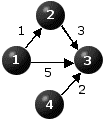
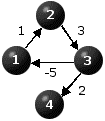
Figure 1 depicts three instances illustrating these cases. The cities are represented by the nodes and the distances are displayed on the directed arcs of the graphs. In all three cases n=4. The respective distance matrices are also provided. The symbol "*" represents infinity so the implication of D(i,j)="*" is that there is no direct link connecting city i to city j.
 |
 |
 |
| D(i,j) | 1 | 2 | 3 | 4 |
| 1 | * | 1 | 5 | * |
| 2 | * | * | 3 | * |
| 3 | * | * | * | 2 |
| 4 | * | * | * | * |
|
| D(i,j) | 1 | 2 | 3 | 4 |
| 1 | * | 1 | 5 | * |
| 2 | * | * | 3 | * |
| 3 | * | * | * | * |
| 4 | * | * | 2 | * |
|
| D(i,j) | 1 | 2 | 3 | 4 |
| 1 | * | 1 | * | * |
| 2 | * | * | 3 | * |
| 3 | -5 | * | * | 2 |
| 4 | * | * | * | * |
|
| a | b | c |
|
Figure 1
By inspection we see that the problem depicted in Figure 1(a) has a unique optimal path, that is x=(1,2,3,4), whose length is equal to 6. The problem depicted in Figure 1(b) does not have a feasible - hence optimal - solution. Figure 1(c) depicts a problem where there is no optimal solution because the length of a path from node 1 to node 4 can be made arbitrarily small by cycling through nodes 1,2 and 3. Every additional cycle will decrease the length of the path by 1.
Observe that if we require the feasible paths to be simple, namely not to include cycles, then the problem depicted in Figure 1(c) would be bounded. Indeed, it would have a unique optimal path x=(1,2,3,4) whose length is equal to 6. In our discussion we do not impose this condition on the problem formulation, namely we admit cyclic paths as feasible solutions provided that they satisfy the precedence constraints. Thus, x'=(1,2,3,1,2,3,4) and x"=(1,2,3,1,2,3,1,2,3,4) are feasible solutions for the problem depicted in Figure 1(c). This is why in the context of our discussion this problem does not have an optimal solution.
Let C={1,2,...,n} denote the set of cities and for each city j in C let P(j) denote the set of its immediate predecessors, and let S(j) denote the set of its immediate successors, namely set
| |
P(j) = {k in C: D(k,j) < infinity} , j in C |
(1) |
| |
S(j) = {k in C: D(j,k) < infinity} , j in C |
(2) |
Thus, for the problem depicted in Figure 1(a), P(1)={}, P(2)={1}, P(3)={1,2}, P(4)={3}, S(1)={2,3}, S(2)={3}, S(3)={4}, S(4)={}, where {} denotes the empty set.
Also, let NP denote the set of cities that have no immediate predecessors, and let NS denote the set of cities that have no immediate successors, that is let
| |
NP = {j in C: P(j) = {}} |
(3) |
| |
NS = {j in C: S(j) = {}} |
(4) |
Thus, in the case of Figure 1(a), NP={1} and NS={4}. Obviously, if city 1 is in NS and/or city n is in NP then the problem is not feasible.
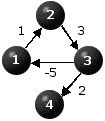
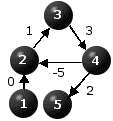
For technical reasons it is convenient to assume that P(1) = {}, namely that city 1 does not have any immediate predecessors. This is a mere formality because if this condition is not satisfied, we can simply introduce a dummy city and connect it to city 1 with a link of length 0. We can then assume that this dummy city - rather than city 1 - is the home city. This minor modelling issue is illustrated in Figure 2.
 |
 |
| D(i,j) | 1 | 2 | 3 | 4 |
| 1 | * | 1 | * | * |
| 2 | * | * | 3 | * |
| 3 | -5 | * | * | 2 |
| 4 | * | * | * | * |
|
| D(i,j) | 1 | 2 | 3 | 4 | 5 |
| 1 | * | 0 | * | * | * |
| 2 | * | * | 1 | * | * |
| 3 | * | * | * | 3 | * |
| 4 | * | -5 | * | * | 2 |
| 5 | * | * | * | * | * |
|
| a | b |
|
Figure 2
The two problems are equivalent in the sense that the problem of finding an optimal path from city 1 to city 4 in Figure 2(a) is equivalent to the problem of finding an optimal path from city 1 to city 5 in Figure 2(b). There is a one to one correspondence between the feasible - therefore optimal - solutions to these two problems.
So with no loss of generality we assume that P(1)={}.
A variety of methods and algorithms are available for the solution of shortest path problems. You can use the following on-line module to experiment with a general purpose algorithm based on the successive approximation method that we briefly discuss in Appendix A.
Module 1
In anticipation of the discussion on classification of shortest path problems and the related algorithmic issues, we note that this module computes the lengths of the shortest paths from node 1 to all other nodes. It can handle cyclic and acyclic problems and it does not care much whether the distances are negative or non-negative. This flexibility and versatility is not due to an algorithmic breakthrough but merely a reflection of the fact that, as stated above, we do not exclude cyclic paths. In other words, we do not restrict the feasible paths to be simple: we do allow feasible path to include cycles. This means that even though there are only finitely many cities, if the distances are allowed to be negative and there is a cycle whose length is negative, then the length of the shortest path could be unbounded from below. The module detects such cases.
This is perhaps an appropriate place to say something about the seemingly odd notion of negative distances.
It must be stressed that this is not an odd notion at all because the term distance is used here as a metaphor. There are many practical problems where the term distance represents costs and/or benefits, and in this context it is very natural to talk about positive and negative distances within the framework of the same problem.
It should be stressed that the term shortest path problem itself is a metaphor. Many optimization problems that have nothing to do with 'real' shortest path problems. For example, the classical knapsack problem, equipment replacement problem, production lot sizing problem, and investment planning problem all have very simple and natural shortest path representations (see for instance Evans and Minieka [1992]). In fact, as was already mentioned above, any combinatorial optimization problem having finitely many feasible solutions can be formulated as a shortest path problem. In this extremely general context the notion of negative distances is not odd at all.
there are cases where the original problem we attempt to solve possesses only non-negative distances but the method used to solve it generates and solves (on the fly) other (related) shortest path problems whose distances can be negative. This is the case, for example, in networks problems where the objective function is the ratio of two functions (eg. see Lawler [1976, pp. 94-97]).
There are many practical situations where we are interested in the longest rather than shortest path. For example, the Critical Path Method (CPM) is based on the detection of longest paths in project networks (Daellenbach et al [1983], Markland and Sweigart [1987], Hillier and Lieberman [1990], Winston [2004]). If we apply the old trick of multiplying the objective function by -1 to transform a maximization problem into an equivalent minimization problem, then we would multiply all the distances by -1. Thus if originally the distances are all positive, after the transformation they will all be negative. The equivalent minimization problem would then have negative distances.
For these reasons, allowing the inter-city distances to be negative is not an eccentric idea. Rather it is a reflection of the fact that many important shortest path problems do possess this feature. Therefore, the interest in algorithms capable of solving shortest path problems whose distances are allowed to be negative is not merely academic in nature.
In the next section we take a quick look at two common OR/MS paradigms for the development of algorithms for the solution of shortest path problems.
To appreciate the role that Dijkstra's Algorithm plays in the analysis and solution of shortest path problems and where it fits into the OR/MS curriculum, it is instructive and constructive to distinguish between the various types of algorithms available for the solution of this important generic problem. There are of course a number of ways to classify such algorithms. Our classification is very much OR/MS and methodologically oriented: it distinguishes between dynamic programming inspired algorithms and linear programming inspired algorithms. We stress that other classification schemes are used both in the computer science and operations research literature (eg. label-setting vs label correcting methods, Bertsekas [ 1991, pp. 67-68], Evans and Minieka [1992, p. 82]). By the same token, as we shall see, these two broad classes can be refined into sub-classes.
Linear programming algorithms
It is not difficult to formulate the shortest path problem as a linear programming problem. In particular, a very common approach is to formulate it as a linear network flow problem. This produces specialized linear programming problems that can then be solved by specialized (efficient) versions of the simplex method (Ford and Fulkerson [1962], Dantzig [1963], Bertsekas [ 1991], Evans and Minieka [1992], Ahuja et al [1993], Winston [2004]).
For example, if the shortest path problem is acyclic and has non negative distances, it can be regarded and formulated as a transhipment problem: City 1 is a supply city, city n is a demand city and all other cities {2,...,n-1} are transhipment cities (they do not produce anything nor do they consume anything). The total supply is equal to the total demand and can be set arbitrarily to 1 unit. If our product is say a small grand piano, the question then becomes: what is the minimum cost of transhipping one small grand piano from city 1 to city n? A cost matrix specifies the cost of shipping one item (small grand piano) from city i directly to city j.
More generally, the shortest path problem can be formulated as a minimum cost network flow problem. The linear programming model is as follows. Let
| |
xij = | Quantity (flow) sent along the link from city i to city j; i,j=1,2,...,n |
|
(5) |
Then the minimum cost network flow problem is as follows:
| | |
min Sijcijxij |
|
(6) |
| | s.t. |
|
|
|
| | |
Skxjk - Sixij = sj , j=1,2,...,n |
|
(7) |
| | |
xij>=0 ; i,j=1,...,n |
|
(8) |
where sj denote the (net) supply at node (city) j on the network and the cost coefficient cij represents the cost of sending one unit of flow along the arc connecting node i to node j. Here S is assumed to enumerate its index/indices over the range {1,...,n}, so for example Skxjk = xj1 + ... + xjn. Note that (7) is a conservation of flow constraint: at each node total inflow = total outflow.
In the case of the shortest path problem we set cij = D(i,j), s(1)=1, s(n)=-1 and s(j)=0 for j=2,...,n-1.
Needless to say, because LP software is so pervasive in OR/MS, the LP paradigm for the shortest path problem has a major attraction for academics, students and practitioners alike.
Dynamic programming algorithms
Algorithms of this type are inspired by the famous Bellman's [1957, p. 83] Principle of Optimality:
| An optimal policy has the property that whatever the initial state and initial decision are, the remaining decisions must constitute an optimal policy with regard to the state resulting from the first decision. |
Guided by this principle, the first thing we do is generalize our shortest path problem (find an optimal path from city 1 to city n) by embedding it in a family of related problems (find an optimal path from city 1 to city j, for j=1,2,3,...,n). So in a typical dynamic programming manner we let
| |
f(j) := length of the shortest path from node 1 to node j, | , j=1,2,3,...,n. |
(9) |
It is important to stress that our objective is to determine the value of f(n). The values of {f(j), j=1,2,...,n-1} are introduced not necessarily because we are interested in them, but first and foremost because this is the way dynamic programming works: in order to determine the value of f(n) it might be necessary to determine the values of f(j) for j=1,2,...,n-1 as well.
In any case, using the above definition of f(j), the following is one of the immediate implications of the principle in the context of the shortest path problem:
Corollary 1
| |
f(j) = D(k,j) + f(k) , for some city k in P(j) |
|
(10) |
for any city j such that P(j) != {}, where != denotes "not equal to".
Of course, algorithmically speaking, this result is not completely satisfactory because it does not identify precisely the value of k for which (10) holds. It merely guarantees that such a k exists and that it is an element of set P(j).
However, conceptually this is just a minor obstacle. After all, f(j) denotes the shortest distance from node 1 to node j and therefore as such it is obvious that the mysterious k on the right hand side of (10) can be identified by making the right hand side of (10) as small as possible. This leads to:
Corollary 2
| |
f(j) = min {D(k,j) + f(k): k in P(j)} , if P(j) != {}. |
|
(11) |
| |
f(j) = Infinity , if P(j) = {} and j > 1. |
|
(12) |
| |
f(1) = 0 , (We assume that P(1)={}). |
|
(13) |
This is the dynamic programming functional equation for the shortest path problem.
It should be stressed that, here and elsewhere, the dynamic programming functional equation does not constitute an algorithm. It merely stipulates certain properties that function f defined in (9) must satisfy. Indeed, in the context of Corollary 2 it constitutes a necessary optimality condition. This point is sometime not appreciated by students in their first encounter with dynamic programming. Apparently this is a reflection of the fact that in many 'textbook examples' the description of the algorithm used to solve the functional equation is almost a carbon copy of the equation itself.
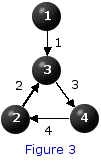
Exercise 1 Solve the dynamic programming functional equation associated with the shortest path problem depicted in Figure 3. For your convenience the system of equations is provided:
 |
|
f(1) = 0
f(2) = 4 + f(4)
f(3) = min {2 + f(2), 1 + f(1)}
f(4) = 3 + f(3)
|
Note that the purpose of the exercise is not merely to find a solution to this system. After all, it is obvious (by inspection) that f(1)=0; f(2)=8; f(3)=1;f(4)=3 is a solution. Rather, the purpose is to highlight the fact that the system itself does not constitute a procedure for determining the values of {f(j): j=1,2,3,4} associated with this system.
And this brings us back to the algorithmic aspects of the shortest path problem: how do we solve (11)-(13)? What kind of algorithms are available for this purpose?
In summary, dynamic programming algorithms for the shortest path problem are procedures designed to determine the values of {f(j)} defined in (9) by solving the dynamic programming functional equation (11)-(13).
Remark: It is possible to formulate a linear programming model for the shortest path problem that is much more intimately related to the dynamic programming functional equation (11)-(13). Hint: construct the dual of (6)-(8) (See Lawler [1976, pp. 78-82] for details concerning the relationship between this formulation and a number of algorithms for the shortest path problem).
In conclusion then, there are different algorithmic approaches for the solution of the shortest path problem (eg. linear programming, dynamic programming). Our mission being what it is, the first question that comes to mind at this stage is obviously: Is Dijkstra's Algorithm a dynamic programming inspired algorithm? A network flow inspired algorithm? Or perhaps an algorithm of another type altogether?
The following quote from an IBM advertisement of their OSL package may serve as a clue to the answer:
| Ants don't need Dijkstra's algorithm to find the shortest path to the picnic. They always find their way, selecting the fastest route, overcoming obstacles, maximizing return with minimum effort. Near perfect utilization of resources with maximum benefit; completing herculean tasks with unparalleled cooperation and teamwork. Wouldn't it be nice if your software could do the same?
OR/MS Today, 29(1), p. 37, 2002 |
|
Another algorithmic issue that must be addressed is the type of shortest path problems that a given algorithm can solve. In anticipation of this, we mention the following classes of shortest path problems:
- Acyclic problems: there are no feasible subpaths that commence and terminate at the same city.
- Cyclic problems: there are feasible subpaths that commence and terminate at the same city.
- Non-negative distance problems: the inter-city distances are non-negative. That is, D(i,j) >=0 for all i and j.
- Negative distance problems: some of the inter-city distances are negative. That is, D(i,j) < 0 for some i and j.
- Non-negative cyclic problems: cyclic problems with the property that the length of all cycles is non-negative (eg. Figure 3).
- Negative cyclic problems: cyclic problems with the property that the length of at least one cycle is negative (eg. Figure 2(b)).
Note that the Cyclic/Acyclic property is determined by the sets {P(j)} whereas the Negative/Nonnegative distance property is determined by the values of the distance matrix D.
And to complicate things even further, there is the question of source/destination pairs. In some problems it is required to find the shortest paths between all pairs of cities. Of course, we can apply repeatedly an algorithm designed for a single pair of cities to handle such multiple-pair problems, but this is not necessarily the best way to deal with the problem.
And finally, there is the very important issue of computational efficiency. How efficient/inefficient is a given shortest path algorithm? What impact the above six properties have on the computational efficiency of shortest path algorithms?
With this in mind let us examine the structure of Dijkstra's Algorithm and the type of shortest path problems that it is capable of solving.
From a purely technical point of view Dijkstra's Algorithm can be described as an iterative procedure inspired by (10) that repeatedly attempts to improve an initial approximation {F(j)} of the (exact) values of {f(j)}. The initial approximation is simply F(1)=0 and F(j)=infinity for j=2,...,n. The details are as follows.
Each city is processed exactly once according to an order to be specified shortly. City 1 is processed first. A record (set) is kept of the cities that are yet to be processed, call it U. So initially U = C = {1,...,n}. When city k is processed the following task is performed:
| |
Update F: set F(j) = min{F(j),D(k,j) + F(k)}, for all j in U/\S(k) |
(14) |
where A/\B denotes the intersection of sets A and B. Recall that S(j) denotes the set of immediate successors of city j. Thus, when city k is processed, the {F(j)} values of its immediate successors that have not yet been processed are updated in accordance with (14).
To complete the informal description of the algorithm it is only necessary to specify the order in which the cities are processed. This is not difficult: the next city to be processed is one whose F(j) value is the smallest over all the unprocessed cities:
| |
Update k: k = arg min {F(j): j in U} |
|
(15) |
recalling that U denotes the set of unprocessed cities. Thus, initially U = {1,...,n} and then after city k is processed it is immediately deleted from U. Formally then
We note in passing that the reason that Dijkstra's Algorithm is regarded as a Greedy method lies in the rule it deploys, (15), to select the next city to be processed: the next city to be processed is the one that is nearest to city 1 among all cities that are yet to be processed.
So putting these three pieces together, here is a more formal description of Dijkstra's Algorithm:
Dijkstra's Algorithm: Version 1
(Determine the value of f(n))
Cycles are welcome, but negative distances are not allowed)
| Initialization: | k=1; F(1) = 0 ; F(j) = Infinity, j=2,...,n ; U = {1,...,n}. |
| Iteration: | While ((k !=n) and (F(k) < infinity)) Do:
Update U: U = U\{k}
Update F: F(j) = min {F(j),D(k,j) + F(k)}, j in U/\S(k)
Update k: k = arg min {F(j): j in U}
End Do. |
|
This means that the algorithm terminates if either the destination city n is next to be processed (k = n) or F(k) = infinity. The latter implies that at this iteration F(j) = infinity for all cities j that have yet to be processed and the conclusion is therefore that these cities cannot be reached from city 1.
Note that the above formulation of the algorithm does not explain how tours are constructed. It only updates the length of tours. The construction of tours can be easily incorporated in this formulation by recording the best immediate predecessor of the city being processed. This predecessor is updated on the fly as F(j) is being updated.
The main result is as follows:
Theorem 1
Dijkstra's Algorithm terminates after at most n-1 iterations. If the distance matrix D is not negative and the algorithm terminates because k=n, then upon termination F(n)=f(n) and furthermore F(j)=f(j) for all j in C for which f(j)<f(n). If termination occurs because F(k) = infinity, then F(j)=f(j) for all j in C for which f(j) < Infinity and f(j)=infinity for all other cities.
In short, if the inter-city distances are not negative the algorithm yields the desired results. The following example illustrates the algorithm in action and highlights the fact that if the distances are allowed to be negative the algorithm may generate a non-optimal solution.
Example 1
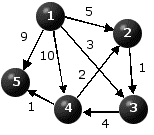
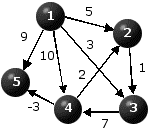
Table 1 displays the results generated by Dijkstra's Algorithm for the two problems depicted in Figure 4. The values in the k, U, F columns are the values of the respective objects at the end of the respective iteration. Iteration 0 represents the initialization step.
 |
 |
| D(i,j) | 1 | 2 | 3 | 4 | 5 |
| 1 | * | 5 | 3 | 10 | 9 |
| 2 | * | * | 1 | * | * |
| 3 | * | * | * | 4 | * |
| 4 | * | 2 | * | * | 1 |
| 5 | * | * | * | * | * |
|
| D(i,j) | 1 | 2 | 3 | 4 | 5 |
| 1 | * | 5 | 3 | 10 | 9 |
| 2 | * | * | 1 | * | * |
| 3 | * | * | * | 7 | * |
| 4 | * | 2 | * | * | -3 |
| 5 | * | * | * | * | * |
|
| a | b |
| |
Figure 4
| Iteration | k | U | F |
| 0 | -- | {1,2,3,4,5} | (0,*,*,*,*) |
| 1 | 1 | {2,3,4,5} | (0,5,3,10,9) |
| 2 | 3 | {2,4,5} | (0,5,3,7,9) |
| 3 | 2 | {4,5} | (0,5,3,7,9) |
| 4 | 4 | {5} | (0,5,3,7,8) |
|
| Iteration | k | U | F |
| 0 | -- | {1,2,3,4,5} | (0,*,*,*,*) |
| 1 | 1 | {2,3,4,5} | (0,5,3,10,9) |
| 2 | 3 | {2,4,5} | (0,5,3,10,9) |
| 3 | 2 | {4,5} | (0,5,3,10,9) |
|
| a | b |
Table 1
Note that in case (b) the algorithm failed to generate an optimal solution: F(n) = F(5) = 9 > f(n) = f(5) = 7.
As far as computational complexity is concerned, Dijkstra's Algorithm performs rather well. For the worst case analysis we can let S(j) = C = {1,...,n} and therefore at the m-th iteration we have |U(m)| := n-m for the Update F and Update k steps of the algorithm, where |A| denotes the cardinality of set A. For simplicity we assume that the min operation in the Update k step is conducted naively by pair-wise comparison. This means that at the m-th iteration the Update k step requires n-m-1 comparisons. Table 2 summarizes the number of additions and comparisons conducted in the Update F and Update k steps of Dijkstra's Algorithm as a function of |U(m)| = n-m, m=1,...,n-1. Summing these values over m=1,...,n-1 yields the total number of operations performed by the algorithm under the worst case scenario.
| | Additions | Comparisons |
| Update F(m) | n-m | n-m |
| Update k(m) | 0 | n-m-1 |
| Total (m=1,...,n-1) | n(n-1)/2 | n(n-1) |
Table 2
So in the worst case, the algorithm executes n(n-1)/2 additions and n(n-1) comparisons and the complexity of the algorithm is therefore O(n2). It should be noted though that special data structures (eg heaps and buckets) can be used to significantly speed up the "arg min" operation conducted by the Update k step of the algorithm (Denardo and Fox [1979], Gallo and Pallottino [1988], Bertsekas [1991], Ahuja et al [1993], Denardo [2003]).
Sometime it is required to determine the shortest distance from city 1 to every other city j, j=2,3,...,n. In this case the "While (...)" clause in Version 1 of the algorithm can be changed to "While (|U| > 1 and F(k) < Infinity)". This yields the more familiar formulation of the algorithm:
Dijkstra's Algorithm: Version 2
(Determine the value of f(j), j=1,...,n)
Cycles are welcome, but negative distances are not allowed
 Initialize: Initialize: | k=1; F(1) = 0; F(j) = Infinity, j=2,...,n
U = {1,2,3,...,n} |
| Iterate: | While (|U| > 1 and F(k) < infinity) Do:
|
 |
U = U\{k} |
 |
F(j) = min {F(j),D(k,j) + F(k)}, j in U/\S(k) |
 |
k = arg min {F(i): i in U} |
| |
End Do.  |
|
You may now wish to experiment with this algorithm using Module 2. Note that the module updates the values of F(j) in two steps. First, the values of G(k,j) = D(k,j) + F(k) are computed for j in U/\S(k) and then the respective values of F(j)=min {F(j),G(k,j)} are computed.
Module 2
Note that the algorithm terminates either when only one city remains to be processed (|U| = 1) and/or when F(j) is equal to infinity for all j in U. The latter indicates that all the cities yet to be processed are not reachable from city 1.
Exercise 2 Construct an example where the algorithm does not yield an optimal solution.
One of the important properties of Dijkstra's Algorithm is that if the distances are non-negative then the cities are processed in non-decreasing order of {f(j)}. That is, if f(j) < f(m) then city j is processed prior to city m and consequently F(j)=f(j) is confirmed prior to F(m)=f(m). This means that if the cities are relabelled as they are being processed (using the k = arg min {F(j): j in U} rule), then upon termination the sequence (F(1),F(2),...,F(n)) would be non-decreasing. The following example illustrates this feature of the algorithm.
Example 2
Consider the shortest path problem depicted on the grid of Module 3. The cities are represented by black squares. The red square in the center of the grid represents the home city. The distances between cities are Euclidean, rounded-off to integer values, except that if the Euclidean distance is greater than some critical value (called radius), the distance is set to be equal to infinity, meaning that the two cities are not connected by a direct link. Also, for simplicity the distance between a city to itself, D(j,j), is set to infinity. The distance matrix is therefore symmetric, hence the graph representing the problem is cyclic and the distances are positive. To highlight the cities connected to a given city by direct links, place the mouse over the city (it is not necessary to click the mouse).
As the algorithm runs, the color of the squares representing the cities changes from black to blue as the cities are being processed. Cities that have been updated but have not yet been processed are colored gold. The pattern to observe is that the blue squares (processed cities) are spreading from the center of the grid outward.
Module 3
 Note that in this particular example the distances are non-negative hence Dijkstra's Algorithm generates the optimal solution. Cities that are not reachable from the home city are also identified (black squares on termination).
Note that in this particular example the distances are non-negative hence Dijkstra's Algorithm generates the optimal solution. Cities that are not reachable from the home city are also identified (black squares on termination).
The grid in this module was made deliberately small (11x11) so that the article could be loaded quickly over the network. As a result, the illustration itself is not as effective as it should be. For this reason we provide a stand-alone module that can generate much larger grids (up to 40x40) and thus can do a much better job illustrating how Dijkstra's Algorithm expands the set of processed cities in an outward direction from the home city. Although this module is very light, it can easily generate and solve problems with hundreds of cities. However, before you attempt to solve large problems, experiment with small problems to check that your computer can cope with larger problems.
It is very difficult to resist the temptation to fiddle with Dijkstra's Algorithm with the view to make it more efficient and/or expand its scope of operation. It is not surprising therefore that since its birth in 1959 the algorithm has been the subject of numerous refinements and modifications as well as numerical experiments. This brought about significant improvements in the performance of the algorithm especially due to the use of sophisticated data structures to handle the (computationally expensive) greedy selection rule k = arg min {F(i): i in U} (Gallo and Pallottino [1988]).
However, as was indicated by Dreyfus [1969] a long time ago, the literature is also spotted with misrepresentations, misinterpretations and plain errors regarding certain aspects of algorithms for the shortest path problem, including Dijkstra's Algorithm. It is important therefore for lecturers to draw their students' attention to this historical fact. For the purposes of our discussion it is sufficient to briefly mention the following:
Negative Distances: For obvious reasons it is only natural to attempt to modify Dijkstra's Algorithm to make it capable of handling problems with negative distances. Consider then the following:
Modified Dijkstra's Algorithm
for
f(j) = min {D(k,j) + f(k): k in P(j)}, j=2,...,n; f(1)=0
Negative distances are welcome, cycles are welcome, negative cycles are not allowed!
| Initialize: |
F(1)=0
F(j) = infinity, j=2,...,n
U={1} |
| Iterate: | While (U != {}) Do:
j = arg min{F(i): i in U}
U = U\{j}
For (k in S(j)) Do:
G = min{F(k),D(j,k) + F(j)}
if(G < F(k)) then {F(k) = G; U = U \/ {k}}
End Do.
End Do. |
|
Note that there are two difference between this procedure and Version 2 of Dijkstra's Algorithm. First, here in each iteration we attempt to improve the values of {F(k)} for all k in S(j), rather than only the values of {F(k)} for k in U^S(j). Second, here we append city k to U whenever there is an improvement (reduction) in the value of F(k). This means that some cities may be processed more than once.
Although these modifications do their job in the sense that the modified scheme can handle negative distances (provided no negative cycles exist), this is achieved at a substantial price as far as performance is concerned. Indeed, (Johnson [1973, p. 385]) advises us that "... This modified algorithm, however, must be used with care ... ". Apparently the warning was issued in response to a claim in Edmonds and Karp [1972] that the worst-case complexity of this modified algorithm is O(n3). Johnson [1973] shows that this assertion is wrong by providing a simple recipe for generating problems in the context of which the complexity of the modified algorithm is a disappointing O(n2n). This is due to the fact that, in the context of these problems, Dijkstra's greedy selection rule admits new cities for processing in the "wrong" order so that some of the cities are processed many times. In fact, there are 2n-1 admissions to set U in the course of the algorithm. Thus, the complexity here is not due to the "arg min" operation which under a naive implementation will require O(n) comparisons per application, but rather is caused by the sheer number of times that some cities re-enter set U: on average each city is processed (2n-1/n) times. Recall that in the context of Dijkstra's original algorithm each city is processed at most once.
Table 3
The message is then that there is no known quick-fix to Dijkstra's Algorithm with regard to handling of negative distances. The point here is not simply that the modified Dijkstra's Algorithm is inferior to a number of well established O(n3) algorithms for handling negative distances. Rather, the point is that the performance of the modified algorithm can be extremely bad in the context of some problems.
Two-trees (bi-directional) Algorithms: It is apparently tempting to argue that the performance of dynamic programming algorithms for the shortest path problem in general and Dijkstra's Algorithm in particular could be enhanced by applying a two-sided, namely a bi-directional, strategy. That is, instead of moving from the origin to the destination, as done by conventional "one-sided" methods, how about moving simultaneously from the origin to the destination and from the destination to the origin? Over the years I have heard spontaneous suggestions along similar lines from students.
It is therefore important to set the record straight on this particular very popular modification of Dijkstra's Algorithm.
Dreyfus [1969] raises the following two issues with regard to this seemingly intuitive idea.
Correctness: Termination conditions of such a procedure must be handled with care. In particular, if the two-sided procedure is terminated as soon as a node has been processed from both directions, then - contrary to some claims made in the literature (eg. Berge and Ghouila-Houri [1965, p. 176]) - there is no guarantee that this node is on an optimal path from the home city to the destination. The example depicted in Figure 6 illustrates this point (Dreyfus [1969, Figure 1, p. 398]).
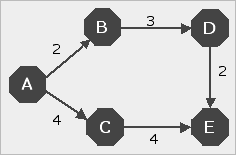
Figure 5
Starting from node A, Dijkstras' Algorithm will first process node A, then node B, then node C, then D, then node E. Starting from node E, and going towards node A, Dijkstra's Algorithm will first process node E, then node D, then node C, then node B, then node A. This means that node C will be the first node to be processed from both sides. Yet, (A,C,E) is not the shortest path from A to E.
For the record it must be stressed that Berge and Ghouila-Houri's [1965] bi-directional approach is applied to Dantzig's [1960] algorithm, not Dijkstra's Algorithm.
Exercise 3 Suggest a correct termination procedure for the two-sided version of Dijkstra's Algorithm. Hint: see Dreyfus [1969, pp. 398-9] for inspiration and references and Bertsekas [ 1991, Exercise 3.8, p. 86] for a detailed outline of a proper termination procedure. Note that Nicholson [1966] is credited for formulating the first correct termination procedure for the two-sided approach. Interestingly, Nicholson's paper has no reference to Dijkstra's Algorithm!
Efficiency: As argued by Dreyfus [1969, p. 399], for the two-sided method to be more efficient than the one-sided method, termination of the former must occur long before all the nodes have been processed (from either direction). If, on the other hand, termination occurs when almost all the nodes have been processed, the two-sided method will not be efficient.
Extensive numerical experiments (eg. Pohl [1971], Helgason et al [1993]) indicate that the two-sided approach performs well in the context of some randomly generated networks. It should be stressed in class that this does not mean, however, that the two-sided method is superior to the one-sided method in other cases.
Exercise 4 (a) Construct a class of shortest path problems where the one-sided method is much more efficient than the two-sided method (b) Explain why the two-sided method tend to perform well in the context of randomly generated networks (Hint: see discussion in Smith [2003] ).
It should also be pointed out that, by its very nature, the two-sided method is designed for cases where an optimal path is sought from a given city to a given city and it cannot be easily modified (and remain efficient) in the context of problems where optimal paths are sought from a given city to a number of (eg. all) other cities. Details on strategies for implementing (general) bi-directional searches can be found in Pohl [1971].
Lecturers teaching Dijkstra's Algorithm may find the following tips useful.
It is customary to illustrate in class how Dijkstra's Algorithm works by graphical animations that highlight the fact that at each stage of the algorithm there are three types of nodes (cities):
- Nodes that have already been processed (F(j)=f(j) has been confirmed)
- Nodes that have been updated at least once but have not yet been confirmed (F(j) < infinity)
- Nodes that have not been updated yet (F(j) = infinity).
Such animations describe the order in which nodes are moved from one class to another, how the {F(j)} values are being updated and how the optimal path from node 1 to the other nodes are constructed as the {F(j)} values are being updated.
We point out that it is instructive to include in such animations two copies of the network - corresponding to two consecutive iterations of the algorithm - so that students can clearly see the changes made at each step of the algorithm.
The following module was designed with these objectives in mind. The {F(j)} values are displayed in the nodes as they are being updated. The spanning tree comprising optimal paths from the origin to the other nodes is constructed on the fly as the {F(j)} values are being updated. It consists of two branches whose arcs are painted blue on the networks.
Minty [1957] proposed a simple 'physical analogue' procedure for solving the shortest path problem when the distance matrix is symmetric and non-negative (assume that Los Angeles is the home city and Boston is the destination) :
Build a string model of the travel network, where knots represent cities and string lengths represent distances (or costs). Seize the knot 'Los Angeles' in your left hand and the knot 'Boston' in your right and pull them apart. If the model becomes entangled, have an assistant untie and retie knots until the entanglement is resolved. Eventually one or more paths will stretch tight - they then are alternative shortest routes.
Dantzig's 'shortest-route tree' can be found in this model by weighing the knots and picking up the model by the knot 'Los Angeles.'
|
This is illustrated in Figure 6. Loose strings represent arcs that are not on any of the optimal paths, hence are not on the shortest-route tree.
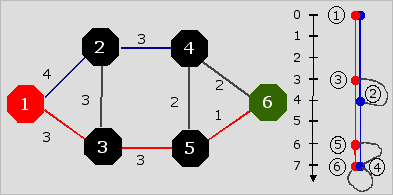
Figure 6
In this example the spanning tree representing the optimal paths consists of two branches (1,2,4) and (1,3,5,6). There are three loose strings representing arc (2,3), arc (4,5) and arc (4,6).
It is important to stress in class that Dijkstra's Algorithm can handle cyclic problems provided that the distances are not negative. This should be reflected in the examples used in class. Surprisingly, in many textbooks and lecture notes the illustrative examples for Dijkstra's Algorithm feature acyclic problems!
By the same token, it is also important to provide students at least one illustrative example where Dijkstra's Algorithm fails to find an optimal solution because of the presence of negative distances in the network.
Students should be advised that there are methods - albeit less efficient - for handling problems with cycles and negative arcs (Ahuja et al [1993], Bertsekas [1991], Evans and Minieka [1992], Lawler [1976]).
Remark: Given the impact of cycles, negative distances and negative cycles on the availability and performance of algorithms for the shortest path problem, it is perhaps not surprising that students (and lecturers ?) are sometime confused with regard to the capabilities of shortest path algorithms, including Dijkstra's Algorithm. The reader is encouraged to read a recent exchange at the SCI.OP-RESEARCH newsgroup (SCI.OP-RESEARCH Digest [2004]) on the capabilities of algorithms for shortest path problems.
In view of the way the {F(j)} are updated in accordance with (14) and the fact that the value of f(n) is determined from the values of {f(j)}, there is obviously a strong resemblance between Dijkstra's Algorithm and conventional dynamic programming algorithms. How come then that this obvious fact has been so often and persistently ignored in the OR/MS and CS literature?
It seems that the answer to this intriguing question lies in the manner in which Dijkstra formulated the algorithm in his original 1959 paper. So it is essential to say a few words now on this paper as far as the exposition of the algorithm is concerned.
The first thing to observe is that the paper is very short (2.5 pages long) and has a pure plain-text format. It contains no mathematical expressions or symbols, no flow charts, no figures. It does not even contain an illustrative example!
Given these features, it is not surprising that the proposed algorithm had not been identified immediately for what it was. The true nature of the algorithm was hidden in the plain-text format of the exposition.
What is more, the term "dynamic programming" is not mentioned at all in the paper and there is not even one single reference to any explicit dynamic programming publication, let alone to
Bellman's [1957] first book on dynamic programming, or any one of his many published dynamic programming articles at that time (The first dynamic programming paper was published in 1952).
Yet, not only is the connection to dynamic programming is definitely there, albeit somewhat hidden, it is substantial and fundamental. To see this it is sufficient to read the first paragraph in the paper dealing with the shortest path problem. It reads as follows (Dijkstra [1959, p. 270] ) :
Problem 2. Find the path of minimum total length between two given nodes P and Q.
We use the fact that, if R is a node on the minimal path from P to Q, knowledge of the latter implies the knowledge of the minimal path from P to R.
|
This is a somewhat cryptic formulation of a typical, common textbook interpretation of Bellman's Principle of Optimality in the context of shortest path problems. For example, in Winston [2004, pp. 967-8] we find a much more informative formulation:
In the context of Example 3, the principle of optimality reduces to the following: Suppose the shortest path (call it R) from city 1 to 10 is known to pass through city i. Then the portion of R that goes from city 1 to city 10 must be a shortest path from city i to city 10.
|
There are other similar interpretations of the principle in the context of the shortest path problem (Eg. Denardo [2003, pp. 14-15]).
In short then, a careful reading of Dijkstra's [1959] original paper leaves no room for doubt:
- Methodologically, Dijkstra's Algorithm for the shortest path problem is based on Bellman's Principle of Optimality.
- Technically, this algorithm constitutes a successive approximation procedure for the solution of the functional equation of dynamic programming associated with the shortest path problem.
In the next section we elaborate on this aspect of Dijkstra's Algorithm.
Given all of this, the following question is unescapable: what is the explanation for the dynamic-programming-free nature of Dijkstra's exposition of his famous algorithm?
Needless to say, we can only speculate on this issue here. But it seems that the following is a reasonable explanation.
As clearly indicated by its title, Dijkstra's paper addressed two problems. The second was the shortest path problem. The first was as follows:
Problem 1. Construct the tree of minimum total length between the n nodes. (A tree is a graph with one and only one path between every two nodes)
|
That is, the first problem addressed by Dijkstra in his famous paper is the famous minimum spanning tree problem.
The similarities between the two problems and the respective algorithms proposed by Dijkstra for their solution and especially Dijkstra's explicit reference to Kruskal's Algorithm (Kruskal [1956]) strongly suggest that Dijkstra regarded his proposed algorithm for the shortest path problem as a modification of Kruskal's Algorithm for the minimum spanning tree problem. This connection may also explain why the referee(s) of his paper did not insist on the inclusion of an explicit reference to dynamic programming in the discussion on the proposed algorithm for the shortest path problem.
An interesting aspect of Dijkstra's discussion on his proposed algorithm for the minimum spanning tree problem is his assertion that " ... The solution given here is to be preferred to the solution given by Kruskal [1] ... ".
And with this in mind let us examine Dijkstra's Algorithm from a dynamic programming point of view: how exactly does Dijkstra's Algorithm fit into the algorithmic framework of dynamic programming?
From a dynamic programming point of view Dijkstra's Algorithm is a procedure for solving the functional equation (11)-(13) in cases where the inter-city distances are non-negative. Cycles are welcome. Since dynamic programming offers a number of methods for solving the functional equation associated with the shortest path problem, it is instructive to relate Dijkstra's Algorithm to these methods.
For the benefit of readers teaching dynamic programming we provide in Appendix A technical details on the relationship between Dijkstra's Algorithm and other methods deployed by dynamic programming for the solution of dynamic programming functional equations. This will enable us to keep the discussion in this section less technical, hence more accessible to readers with limited dynamic programming expertise.
Very broadly, there are two strategies for the solution of dynamic programming functional equations, resulting in two classes of methods, namely
- Direct methods.
- Successive approximation methods.
Direct methods are based on "direct" conversion of the functional equation of dynamic programming into an iterative procedure. Their scope of operation is therefore limited to situations where it is possible to either solve the functional equation recursively or iteratively (non-recursively) in such a manner that while computing the value of f(j) all the relevant values of f(k) on the right hand side of the functional equation have already been computed (somehow). Since a truly recursive implementation is limited to relatively small problems, it follows that for most practical cases the direct approach is limited to cases where the elements of C={1,...,n}, the domain of function f, can be ordered so that for each j in C we have k > j for all k in P(j). This requires the shortest path problem to be acyclic. Conversely, if the problem is acyclic, the cities can be ordered in such a manner.
Not surprisingly, introductory general purpose OR/MS textbooks deal almost exclusively with these methods and use examples where it is easy to arrange the elements of C in a proper order to enable the solution of the functional equation with the aid of direct methods. Perhaps one of the most well known application of this approach is in the context of the Critical Path Method (CPM) where it is used to compute early and late event times which are in fact specialized acyclic longest path problems. Remark: many OR/MS textbooks do not credit dynamic programming for this important application!
In contrast, successive approximation methods do not determine the value of f(j) for a particular value of j by a single application of right-hand side of the functional equation. Rather, an initial approximation for {f(j): j in C} is constructed, and then it is successively updated (improved) either using the functional equation itself or an equation related to it (eg. (10)). The process terminates when a fixed point is reached, namely when no further improvement is possible.
There are many successive approximation methods. They differ in the mechanism they use to update the approximated {f(j)} values and in the order in which these updates are conducted.
In this framework Dijkstra's Algorithm is viewed as a successive approximation method characterized by two properties. One is related to the mechanism used to update the approximated values of {f(j)} and one is related to the order in which these values are updated. Specifically, the updating mechanism is based on (10) or rather its variate (14), and the updating order is based on the "best first" rule (15). Since variates of the former are commonly used in successive approximation, it follows that (15) is actually what really characterizes Dijkstra's Algorithm and makes it different from other dynamic programming successive approximation methods for the shortest path problem.
In summary then, from a dynamic programming perspective Dijkstra's Algorithm is a successive approximation method characterised by a unique order (15) in which the approximated {f(j)} values are updated.
More on this can be found in Appendix A.
In the context of our discussion, two related issues deserve attention in the preparation of courseware dealing with Dijkstra's Algorithm:
- The dynamic programming roots of this algorithm.
- The relationship between this algorithm and other types of algorithms used to solve dynamic programming functional equations.
Needless to say, the manner in which these issues should be handled would depend very much on the specific objectives of the courseware, the students' technical background, mode of delivery and many other aspects of the total teaching/learning system. For this reason we do not intend to propose a general purpose recipe for dealing with this generic dilemma.
Instead, we refer the interested reader to Lawler's [1976, Chapter 3] book as an example of how this can be done in a student-friendly manner. In the introduction to the chapter entitled Shortest Paths Lawler states the following (Lawler's [1976, p. 60]):
| The dominant ideas in the solution of these shortest-path problems are those of dynamic programming. Thus, in Section 3 we invoke the "Principle of Optimality" to formulate a set of equations which must be satisfied by shortest path lengths. We then proceed to solve these equations by methods that are, for the most part, standard dynamic programming techniques.
This situation is hardly surprising. It is not inaccurate to claim that, in the deterministic and combinatorial realm, dynamic programming is primarily concerned with the computation of shortest paths in networks with one type of special structure or another. What distinguishes the networks dealt with in this chapter is that they have no distinguishing structure. |
Dijkstra's Algorithm makes its appearance in Section 5 of this chapter, entitled Networks with Positive Arcs: Dijkstra's Method.
In this context it is also appropriate to say something about what should be regarded as an "undesirable" treatment of the dilemma. In particular, there seems to be no justification whatsoever to completely separate the discussion on Dijkstra's Algorithm from the discussion on dynamic programming in the same courseware (eg. textbook). Unfortunately, this happens too often: in many OR/MS and CS textbooks there are no cross-references whatsoever between the dynamic programming section/chapter to the Dijkstra's Algorithm section/chapter. This, we argue should be regarded as "highly undesirable".
Note that we do not argue here that in the case of coursewares dealing with both dynamic programming and Dijkstra's Algorithm the discussion on the latter must be incorporated in the discussion on the former. Rather, what we argue is that in such cases the relationship between the two must be addressed, or at least alluded to.
Regarding coursewares that deal with Dijkstra's Algorithm but do not deal with dynamic programming, students should be advised on the dynamic programming connection and be supplied with appropriate references.
As for dynamic programming coursewares, the point we wish to stress is that Dijkstra's Algorithm is definitely a legitimate dynamic programming "topic" and as such is an appropriate item for inclusion in dynamic programming coursewares. However, the question whether to incorporate Dijkstra's Algorithm in such coursewares must be dealt with on a case by case basis, and the answer should reflect, among other things, the specific orientation of the courseware.
The literature makes is abundantly clear that the procedure commonly known today as Dijkstra's Algorithm was discovered in the late 1950s, apparently independently, by a number of analysts. There are strong indications that the algorithm was known in certain circles before the publication of Dijkstra's famous paper. It is therefore somewhat surprising that this fact is not manifested today in the "official" title of the algorithm.
Briefly: Dijkstra [1959] submitted his short paper for publication in Numerische Mathematik June 1959. In November 1959, Pollack and Wiebenson [1960] submitted a paper entitled Solutions of the shortest-route problem - a review to the journal Operations Research. This review briefly discusses and compares seven methods for solving the shortest path problem. Dijkstra [1959] paper is not mentioned in this review.
However, the review presents a 'highly efficient' method, attributed - as a dateless private communication - to Minty. The procedure is defined as follows (Pollack and Wieberson [1960, p. 225]: The objective is to find the shortest path from city A to city B.):
1. Label the city A with the distance 'zero,' Go to 2.
2. Look at all one-way streets with their 'tails' labelled and their 'heads' unlabelled. For each such street, form the sum of the label and the length. Select a street making this sum a minimum and place a check-mark beside it. Label the 'head' city of this street with the sum. Return to the beginning of 2.
The process may be terminated in various ways: (a) when the city B is labelled, (b) when all cities have been labelled, or (c) when the minimum of the sums is 'infinity.' |
This is none other than Dijkstra's Algorithm!
According to Dreyfus [1976, p. 397], the origin of this algorithm probably dates back to Ford and Fulkerson's work on more general (network flow) problems (eg. Ford and Fulkerson [1958, 1962]).
It is interesting to note that in his paper, Dijkstra [1959, p. 271] refers only to two methods for solving the shortest path problem, namely Ford [1956] and Berge [1958]. As we already indicated, it is extremely odd that there is no reference to dynamic programming in general, and the Principle of Optimality in particular, in this paper.
Another interesting historical fact is that in November 1959 George Dantzig submitted a paper entitled "On the shortest route through a network" for publication in Management Science. This short (3.5 pages) paper (Dantzig [1960]) proposes an algorithm for the shortest path problem in cases where distances from each node can be easily sorted in increasing order and it is easy to ignore certain arcs dynamically. It has no reference to Dijkstra's paper but obviously does have an explicit reference to Bellman's work (Bellman [1958]) - they both worked at the RAND corporation at that time.
The only reference these two papers ( [1959], Dantzig [1960]) have in common is Ford's [1956] RAND report on Network Flow Theory.
Remarks:
- Recently, Dantzig and Thapa [2003, p. 244] pointed out that Dijkstra's Algorithm is a refinement of an algorithm proposed independently by Dantzig about the same time (1959) that Dijkstra published his paper. We cannot confirm this claim because the reference given in Dantzig and Thapa [2003, p. 244] seems not to be the intended one. The intended reference is apparently Dantzig [1960], where Dantzig's famous algorithm for the shortest path problem is proposed. In this case our view is that the two algorithms are substantially different from each other (see also comments in Dreyfus [1976, pp. 398-399]).
- We also note in passing that Dantzig's [1960] paper is credited for being the first to suggest a bi-directional strategy for solving the shortest path problem - albeit not in conjunction with Dijkstra's Algorithm but rather in conjunction with Dantzig's own algorithm. However, Dreyfus [1976, pp. 398-399] points out that Dantzig [1960] does not propose any termination policy for the bi-directional version of his algorithm.
- It is important to stress that the central point in our discussion is not "who was first?" Rather, the issue is the relation between Dijkstra's Algorithm and standard OR/MS methods and how this relationship should be dealt with in OR/MS courseware.
Dijkstra's Algorithm is covered extensively in the OR/MS and CS literature and is a popular topic in introductory OR/MS textbooks. For historical reasons the algorithm is regarded by many as a "computer science" method. But as we have shown in this discussion, this algorithm has very strong OR/MS roots. This is a pity!
Indeed, one of the purposes of this discussion is to point out that this situation can be altered within OR/MS and - it is hoped - also within CS.
OR/MS courseware developers are encouraged to re-consider the way they treat this algorithm and how they relate it to other OR/MS methods and techniques. In particular, this algorithm can be used to illustrate the deployment of successive approximation methods by dynamic programming.
Ahuja, R.K., Magnanti, T.L. and Orlin, J.B. (1993), Network Flow Theory, Algorithms, and Applications, Prentice-Hall, Englewood-Cliffs, NJ.
Bellman, R. (1952), On the theory of dynamic programming, Proceedings of the National Academy of Sciences, 38, 716-719.
Bellman, R. (1957), Dynamic Programming, Princeton University Press, Princeton, NJ.
Bellman, R. (1958), On a routing problem, Quarterly of Applied Mathematics, 16(1), 87-90.
Berge, C. (1958), Theorie des Graphes et ses Applications, Dunod, Paris.
Berge, C. and Ghouila-Houri, A. (1965), Programming, Games, and Transportation Networks, John Wiley and Sons, NY.
Bertsekas, D. (1991), Linear Network Optimization, The MIT Press, Cambridge, MA.
Brassard, G. and Bratley, P. (1988) Algorithmics,Prentice-Hall, Englewood Cliffs, NJ.
Cherkassky, B.V., Goldberg, A.V. and Radzik, T. (1994), Shortest paths algorithms: theory and experimental evaluation, pp. 516-525, Proceedings of the fifth annual ACM-SIAM symposium on Discrete algorithms, Arlington, Virginia, USA.
Daellenbach, H.G., George, J.A. and D.C. McNickle, (1983), Introduction to Operations Research Techniques, 2nd Edition, Allyn and Bacon, Boston.
Dantzig, G.B. (1960), On the shortest path route through a network, Management Science, 6, 187-190.
Dantzig, G.B., (1963), Linear Programming and Extensions, Princeton University Press, Princeton, NJ.
Dantzig, G.B. and N.M Thapa, (2003), Linear Programming 2: Theory and Extensions, Springer Verlag, Berlin.
Denardo, E.V. and Fox, B.L. (1979), Shortest-route methods: 1. Reaching, pruning, and buckets, Operations Research, 27, 161-186.
Denardo, E.V. (2003), Dynamic Programming, Dover, Mineola, NY.
Dijkstra, E.W. (1959), A note on Two Problems in Connexion with Graphs, Numerische mathematik, 1, 269-271.
Dreyfus, S. (1969), An appraisal of some shortest-path algorithms Operations Research, 17, 395-412.
Edmonds, J. and Karp, R.M.(1972), Theoretical improvements in algorithmic efficiency for network flow problems, Journal of ACM, 19, 2, 248-264.
Evans, J.R. and Minieka, E. (1992), Optimization Algorithms for Networks and Graphs, Marcel Dekker, NY.
Ford, L.R. (1956), Network Flow Theory, RAND paper P-923.
Ford, L.R. and Fulkerson, D.R. (1958), Consructing maximal dynamic flows from static flows, Operations Research, 6, 419-433.
Ford, L.R. and Fulkerson, D.R. (1962), Flows in Networks, Princeton University Press, Princeton, NJ.
Gallo, G. and Pallottino, S. (1988), Shortest path algorithms, Annals of Operations Research , 13, 3-79.
Gass, S.I. and Harris, C.M. (1996), Encyclopedia of Operations Research and management Science, Kluwer, Boston, Mass.
Helgason, R.V., Kennigton, J.L. and Stewart, B.D. (1993), The one-to-one shortest-path problem: an empirical analysis with the two-tree Hijkstra algorithm, Computational Optimization and Applications, 1, 47-75.
Hillier, F.S. and Lieberman, G.J. (1990) Introduction to Operations Research, 5th Edition, Holden -Day, Oakland, CA.
Johnson, D.B. (1973), A note on Dijkstra's shortest path algorithm, Journal of the Association for Computing Machinery, 20(3), 385-388.
Lawler, E.L. (1976), Combinatorial Optimization: Networks and Matroids, Holt, Rinehart and Whinston, NY.
Markland, R.E. and J.R. Sweigart, (1987), Quantitative Methods: Applications to Managerial Decision Making, John Wiley, NY.
Microsoft Shortest Path Algorithms Project: research.microsoft.com/research/sv/SPA/ex.html.
Minty, E.F. (1957), A comment on the shortest-route problem,Operations research, 5, 724.
Nicholson, T.A.J. (1966), Finding the shortest route between two points in a network,The Computer Journal, 6, 275-280.
Moore, E.F. (1959), The shortest path through a maze, pp. 285-292 in Proceedings of an International Synposium on the Theory of Switching (Cambridge, Massachusetts, 2-5 April, 1957), Harvard University Press, Cambridge.
Pohl, I. (1971), Bi-directional search, in Machine Intelligence, 6, edited by Meltzer B. and Michie, D., 127-140.
Pollack M. and Wiebenson, W. (1960), Solution of the shortest-route problem - a review, Operations Research, 8, 224-230.
SCI.OP-RESEARCH, (2004), Changing minimization to maximization, do the following problems change? SCI.OP-RESEARCH Digest, Volume 11: Issue 13 (Mon, 5 April 2004. The items can be found at : www.deja.com/group/sci.op-research).
Smart, D.R. (1974), Fixed Point Theorems, Cambridge University Press, Cambride.
Smith, D.K. (2003), Networks and Graphs: Techniques and Computational Methods, Horwood Publishing Limited, Chichester, UK.
Sniedovich, M. (1992), Dynamic Programming, Marcel Dekker, NY.
Stuckless, T. (2003), Brouwer's Fixed Point Theorem: Methods of Proof and Applications, M.Sc. Thesis, Department of Mathematics, Simon Fraser University.
Winston, W.L. (2004), Operations Research Applications and Algorithms, Fourth Edition, Brooks/Cole, Belmont, CA.
Broadly speaking, dynamic programming deploys two approaches for the solution of its functional equation, namely direct methods and successive approximation methods. It what follows we briefly describe how these methods are used in the context of the shortest path problem and their relationship to Dijkstra's Algorithm.
Direct Methods
Methods of this type are 'direct' applications of the dynamic programming functional equation. They are used when the shortest path problem is acyclic. For simplicity assume that the elements of C are arranged in increasing order so that for each j in C we have k < j for all k in P(j).
Generic Direct Method
(k < j for all k in P(j), j=1,...,n)
| Initialization: | F(1)=0 |
| Iteration: | For j=2,...,n Do: |
| F(j) = min {D(k,j) + F(k): k in P(j)} |
| End Do |
|
Clearly, upon termination the {F(j)} values constitute a solution to the dynamic programming functional equation (11) and F(j)=f(j) for all j in C.
Exercise 5 Determine the complexity of the algorithm inspired by the Generic Direct Method.
A major limitation of this method is that it cannot be used in cases where the network under consideration is cyclic because in such cases there is at least one pair of distinct cities, say (i,j) such that using the functional equation you cannot compute F(j) before you compute F(i) and you cannot compute F(i) before you compute F(j).
Observe that if the inter-city distances are non-negative, then in computing the value of f(j) using the functional equation, it is not necessary to consider cities k in P(j) for which f(k) > f(j). Hence,
Lemma 1
| |
f(j) = min {D(k,j) + f(k): k in P(j), f(k) < f(j)} |
(17) |
Now, suppose that we re-order the cities so that f(j) is non-decreasing with j, that is f(j+1) >= f(j) for all j=1,...,n-1. Then, we could use the following Generic Direct Method to compute {f(j)}:
Modified Generic Direct Method
(Cycles are welcome, non-negative distances are required, f(j+1) > f(j), j=1,...,n-1)
| Initialization: | F(1)=0 |
| Iteration: | For j=2,...,n Do: |
| F(j) = min {D(k,j) + F(k): k in P(j), k < j} |
| End Do |
|
Clearly, upon termination the {F(j)} values constitute a solution to the dynamic programming functional equation (11) and F(j)=f(j) for all j in C.
Needless to say, this procedure is not very practical because in order to re-order the cities in the manner required it might be necessary to first compute the values of {f(j)}, in which case what is the point of recomputing these values?
Nevertheless, this procedure is instructive in that it suggests that the solution of the dynamic programming functional equation can be carried out not in a topological order (dictated by the precedence constraints), but rather in an order dictated by the values of {f(j)}. This in turn suggests that it might be useful to re-order the cities on the fly (as the functional equation is being solved) rather than as a pre-processing step.
This in turn suggests the deployment of a successive approximation approach for the solution of the functional equation of the shortest path problem that will generate the {f(j)} values in a non-decreasing order.
Successive Approximation Methods
Successive approximation is a generic approach for solving equations and it is used extensively in dynamic programming, especially in cases of infinite horizon sequential decision problems (Bellman [1957], Sniedovich [1992], Denardo [2003]).
In a nutshell, these methods work as follows: an initial approximation to the unknown object of interest (eg. function) is constructed. This approximation is successively updated (hopefully improved) until no further improvement is possible (or until it is determined that the process diverges rather then converges). The various methods differ in the way the updating is carried out and/or the order in which the updating mechanism is conducted.
In the case of the dynamic programming functional equation for the shortest path problem (11)-(13) we regard f as an unknown function on C and approximate it by some function F. We then successively update F using either the dynamic programming functional equation itself or an equation related to it. The updating process is repeated until a solution is found, namely until an approximation F is found that solves the equation governing the updating process.
There are two updating philosophies. To describe the basic ideas behind them and the differences and similarities between them, assume that we currently have a new approximation F for f and that some of the new values of {F(j)} are smaller than the respective previous values. The basic question is then: how do we propagate the improvement in some of the {F(j)} values to other cities?
One approach to tackle the task posed by this question, call it Pull, is inspired by the Generic Direct Method. It uses the functional equation itself to compute new (hopefully improved ) values of {F(j)}. That is,
| |
Pull at j : F(j) = min {D(i,j)+F(i): i in P(j)} , j=2,...,n |
(18) |
Naturally, this operation makes sense only if there was an improvement in at least one element of {F(i): i in P(j)}.
The term Pull is used here to convey the idea that when we apply this operation at city j we have to pull the most recently available values of {F(i): i in P(j)}. This operation is used extensively by dynamic programming in the context of infinite horizon problems in general (Bellman [1957], Sniedovich [1992]) and Markovian decision processes in particular (Denardo [2003])
The other approach to updating, call it Push, propagates an improvement in F(j) to the immediate successors of j. That is, Push capitalizes on the fact that in accordance with the Principle of Optimality, for any city k such that P(k) is not empty we have
for some city j such that k is in S(j).
This suggests the following simple updating recipe:
| |
Push at j : F(k) = min {F(k),D(j,k)+F(j)} , k in S(j) |
(20) |
The term Push conveys the idea that if we observe an improvement (decrease) in the value of F(j) then it makes sense to propagate it to its immediate successors using (20). The improved value of F(j) is thus pushed to the successors of j so that they can check whether this improvement can actually improve their respective {F(k)} values.
The Push operation is commonly used by dynamic programming methods such as Reaching and Label-correcting methods (Denardo and Fox [1979], Bertsekas [ 1991], Denardo [2003]).
The main difference between the Pull and Push operations is that a Pull at j attempt to improve the current value of F(j) whereas a Push at j attempts to improve the current values of {F(k): k in S(j)}.
In either case, to initialize the successive approximation process we need an initial approximation F for f. Ideally, this approximation should be easy to compute, guarantee that subsequent approximations of F will correspond to feasible path lengths and be non-increasing. The approximation F(1)=0 and F(j)=infinity, j=2,...,n can be used for this purpose. This is not a very exciting approximation but it does its job.
A critical issue in the implementation of successive approximation methods for the shortest path problem is the order in which cities are processed. Let U denote the set of cities that need to be processed and let Select_From (U) denote the element of U selected to be processed next. Then the two successive approximation strategies can be described as follows:
Successive Approximation
for
f(j) = min {D(k,j) + f(k): k in P(j)}, j=2,...,n; f(1)=0
Negative distances and non-negative cycles are welcome!
| Pull | | Push |
F(1)=0
F(j)=infinity, j=2,...,n
U=S(1) | Ini
tia
lize |
F(1)=0
F(j)=infinity, j=2,...,n
U={1} |
| |
|
While (U != {}) Do:
j=Select_From (U)
U=U\{j}
G=min{D(k,j)+F(k): k in P(j)}
if(G<F(j)){F(j)=G; U=U\/S(j)}
End Do. | I
t
e
r
a
t
e |
While (U != {}) Do:
j=Select_From (U)
U=U\{j}
For (k in S(j)) Do:
G=min{F(k),D(j,k)+F(j)}
if(G<F(k)){F(k)=G; U=U\/{k}}
End Do.
End Do. |
|
Here and elsewhere \/ denotes the (set) union operation.
Exercise 6 Determine the complexity of Pull and Push algorithms.
Observe that a single Pull operation updates a single F(i) value, that is a Pull at j updates only the value of F(j). In contrast, a single Push operation typically updates several F(k) values, that is a Push at j updates the values of {F(k): k in S(j)}. This is illustrated in Figure 7.
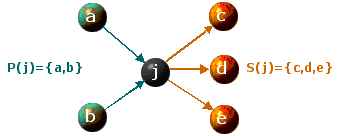 |
| F(j)=min {D(k,j)+F(k): k in P(j)} Pull at j |
, |
F(k)=min{F(k),D(j,k)+F(j)} , k in S(j) Push at j |
|
Figure 7
The difference and similarities between the Pull and Push "philosophies" can be summarized as follows:
f(j) = min {D(k,j) + f(k): k in P(j)}, j=1,...,n
f(1)=0
| Pull | Push |
When city j is processed, the value of F(j) is updated as follows: F(j) = min {D(k,j)+F(k): k in P(j)}
If there is an improvement (decrease) in F(j), the immediate successors of j are appended to the list of cities to be processed (U = U \/ S(j)).
|
When city j is processed, the values of {F(k); k in S(j)} are updated as follows: F(k) = min {F(k),D(j,k)+F(j): k in S(j)}
If there is an improvement (decrease) in F(k), then city k is appended to the list of cities to be processed (U = U \/ {k}).
|
Table 4
Remarks:
- For each j in C the Generic Direct Method computes the value of F(j) exactly once. The two Successive Approximation methods typically compute (update) the value of F(j) several times for a given j.
- Upon termination the Successive Approximation procedures yield solutions to the dynamic programming functional equation. Thus, if the functional equation has a unique solution, the solution generated by an Successive Approximation procedure is optimal.
- If the problem does not possess feasible cycles whose lengths are negative, then the Successive Approximation procedures terminate after finitely many iterations. In particular, termination is guaranteed if the inter-city distances are non-negative.
- If the problem possesses a feasible cycle whose length is negative, the Successive Approximation procedures may not terminate.
Exercise 7 Explain why the Pull at j update is written as
| |
F(j) = min {D(k,j) + F(k): k in P(j)} |
(21) |
rather than as
| |
F(j) = min {F(j),min{D(k,j) + F(k): k in P(j)}} |
(22) |
Exercise 8 Explain why the Push at j update is written as
| |
F(k) = min {F(k),D(j,k) + F(j)}, k in P(j) |
(23) |
rather than as
| |
F(k) = D(j,k) + F(j), k in P(j) |
(24) |
Exercise 9 Modify the Pull and Push schemes to enable them to handle negative cycles.
A quick comparison of the Generic Direct Method with the Successive Approximation approach reveals why it is not surprising that most introductory general purpose OR/MS textbooks do not discuss the latter.
Since clearly Dijkstra's Algorithm is not a direct method, we can now rephrase the central question on our agenda as follows: what kind of Successive Approximation method is it? Is it a Push method or is it a Pull method?
The answer is crystal clear: Dijkstra's Algorithm is a Push-type dynamic programming Successive Approximation method. More specifically, it constitutes an instance of the Push method characterized by
| |
Select_From (U) = arg min {F(i): i in U} |
(25) |
This particular choice for Select_From (U) is fully justified in the context of non-negative distance problems. Among other things, in this context this choice guarantees that each city is processed at most once. Needless to say, this is a very attractive feature and is manifested in the efficiency of the algorithm in the context of problems of this type.
With this in mind, here is another version of Dijkstra's Algorithm that is more in tune with the formulation of Push.
Dijkstra's Algorithm Version 3
for
f(j) = min {D(k,j) + f(k): k in P(j)}, j=2,...,n; f(1)=0
cycles are welcome, non-negative distances are assumed
| Initialize: |
F(1)=0
F(j) = infinity, j=2,...,n
U={1} |
| Iterate: | While (|U| > 1) Do:
j = arg min{F(i): i in U}
U = U\{j}
For (k in S(j), F(k) > F(j)) Do:
G = min{F(k),D(j,k) + F(j)}
if(G < F(k)) then {F(k) = G; U = U \/ {k}}
End Do.
End Do. |
|
Exercise 10 Note that here the updating of F is spelled out in detail by the "For(k in S(j), F(k) > F(j)) Do" block. This is done to enable refinement of the content of U and its updating in line with Push. Identify the difference between the initialization and updating of U here and in Version 2 and explain the rationale for the modification.
The relationship between Push and Dijkstra's Algorithm raises the following interesting Chicken/Egg question: is Push a generalization of Dijkstra's Algorithm or Dijkstra's Algorithm is a specialization of Push?
Be it as it may, from a purely historical point of view Dijkstra's Algorithm is definitely a specialized successive approximation method for solving the dynamic programming functional equation of the shortest path problem. This Push-type specialization exploits the fact that if the inter-city distances are not negative then the choice of the next city to be processed stipulated by j = arg min {F(i): i in U} not only makes sense conceptually, but also performs well in practice, especially if suitable data structures are use to speed up this selection procedure.
In short, from a dynamic programming perspective, Dijkstra's Algorithm can be regarded as a clever application of Push-type successive approximation methods for the solution of the functional equation associated with shortest path problems whose arc lengths are non-negative.
Remark: To keep the discussed focussed and brief we have deliberately avoided relating Dijkstra's Algorithm to Reaching (Denardo [2003]) and label setting (Bertsekas [ 1991], Evans and Minieka [1992]). For the record we note that in the case of cyclic networks with nonnegative distances, Reaching (Denardo [2003, p. 20]) is equivalent to Dijkstra's Algorithm and Dijkstra's Algorithm is clearly a label setting method (Bertsekas [ 1991, p. 68], Evans and Minieka [1992, p. 83]).
We add in passing that Reaching and label setting methods - and for that matter label correcting methods - are all successive approximation methods. Indeed, what they all have in common is that an initial approximation of f is repeatedly updated (improved) until a fixed point of the dynamic programming functional equation is found.
Classroom tip: It is important to advise students that successive approximation methods deployed by dynamic programming are adaptations of a generic successive approximation approach commonly used in the solution of equations. This is particularly important in cases where students are already familiar with other applications of this approach. For the benefit of readers teaching dynamic programming we provide in Appendix B a short discussion on the generic successive approximation approach.
Suppose that we wish to solve the equation h(x)=0 where h is a given real valued function on some given set X. The Successive Approximation approach to this problem is based on the following simple idea: Using the relation h(x)=0, we express x in terms of itself, say as x=g(x), and then we successively update an initial value of x using the equation x=g(x) for this purpose. This yields a sequence {x(j)} such that x(j+1) = g(x(j)). Hopefully, the sequence {x(j)} will converge to some x* in X such that x*=g(x*), hence h(x*)=0. For example, consider the equation
| |
h(x) = x2 -5x + 6 = 0 |
(26) |
To solve this equation via successive approximation we first re-write it as x=g(x). This yields the equivalent equation
| |
x = g(x) := (x2 + 6)/5 |
(27) |
Now, suppose that we use x(0)=0 as the initial approximation. Then this yields
| |
x(1) = g(x(0)) = 6/5 |
(28) |
So according to our scheme
| |
x(2) = g(x(1)) = ((6/5)2 + 6 )/5 = 186/125 |
(29) |
We continue in this manner until we (hopefully) get x(j+1)= x(j), in which case x(j) is a solution, or until we observe (disappointedly) that sequence {x(j)} does not seem to converge.
Exercise 9 Try to generate both roots of the equation h(x) = x2 - 5x + 6 = 0 using the module below. Observe that this equation has two roots namely x=2 and x=3.
Module 5
Exercise 10 Find a solution to the equation x3 = log(1+x2) using the module below.
Module 6
An important aspects of the implementation of successive approximation methods is the choice of an appropriate initial approximation. You are encouraged to use the modules to experiment with this feature.
Of course, equations of the form x = g(x) are sufficiently important on their own, regardless of their origin. If g is a mapping from some set X to itself, then an x in X such that x=g(x) is called a fixed point of g in X. The existence of fixed points is therefore a very important issue in pure and applied mathematics (eg. Smart [1974]). The following is no doubt the most famous result in this area:
Brouwer's Fixed Point Theorem: Let X be a compact convex subset of the n dimensional Euclidean space and let g be a continuous function mapping X into itself. Then there exists a least one x in X such that g(x)=x.
Remark: This theorem is famous not only because it is so important theoretically and so useful practically, but also for being so easy to state but notoriously complicated to prove. Stuckless [2003, p. 4] claims that "... It has been estimated that while 95% of mathematicians can state Brouwer's theorem, less than 10% know how to proof it ..."
It is important to stress the fact that the basic method illustrated above is not inherently numerical in nature. That is, successive approximation procedures can be carried out analytically rather than numerically. By the same token, it should be noted that they can be used to solve functional equations, that is equations whose unknowns are functions rather than scalars.
Exercise 11 Solve the functional equation x(z) = z2 + bx(z/b), where b > 1 is a given constant and x is a real valued function on the non-negative section of the real line. Hint: follow the procedure used below.
Since in general an equation may have more than one solution, it is important to make sure that proper boundary conditions are used to extract the solution of interest. To illustrate this point, consider the functional equation
where b is a given constant in the range (0,1) and q is a real valued function on the non-negative section of the real line.
Formally, the unknown here is a real function q on the non-negative segment of the real line. We start with the trivial approximation q(0) of q given by q(0)(z)=0 for all z. Using this approximation and the prescribed equation (30), we obtain the next approximation
| |
q(1)(z) = z2 + q(0)(bz) = z2 + 0 = z2 |
(31) |
We repeat this process to obtain the next approximation:
| |
q(2)(z) = z2 + q(1)(bz) = z2 + (bz)2 = z2[1+b2] |
(32) |
And the next approximation:
| |
q(3)(z) = z2 + q(2)(bz) = z2 + (bz)2[1+b2] = z2[1 + b2 + b4] |
(33) |
Proceeding by induction, it is not difficult to show that for q(m)(z):= z2 + q(m-1)(bz) we have
| |
q(m)(z) = z2[1 + b + b2 + ... + b2(m-1)] |
(34) |
So at the limit, as m is approaching infinity, we obtain
| |
Q(z) := lim m --> infinity q(m)(z) = z2/ [1-b2] |
(35) |
Exercise 12 Check, by substitution, that the right-hand side expression is indeed a solution to the functional equation of interest (30). Then show that (30) possesses infinitely many solutions. Hint: show that if q(z) is a solution to (30), namely if q(z) = z2 + q(bz) for all z >= 0, then so is s+q(z) for any scalar s.
In cases where the functional equation does not have a unique solution, the solution of interest is obtained by the imposition of relevant boundary conditions. For example, in the case of (30), if we require q(0) =0, then it would follow that Q(z) given by (35) is the unique solution.
Now back to the dynamic programming functional equation of the shortest path problem (11)-(13). In this framework function f is the unknown and the functional equation is used repeatedly to update some initial approximation, say F, of f. The process is repeated until a solution is found, namely until an approximation F is found that solves this equation. A natural choice for the initial approximation is F(1)=0 and F(j) = D(1,j), j =2,...,n.
Note that if the network is acyclic then upon requiring f(1) = 0 and f(j) = infinity for any city j that does not have any immediate predecessor, the dynamic programming functional equation will possess a unique solution. If the problem is cyclic the equation may have more than one solution, in which case it might be necessary to find out which one of these solutions is a solution to the shortest path problem of interest.
Example 3
Consider the shortest path problem associated with the network depicted in Figure 8. Its functional equation is as follows:
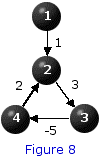 |
|
q(1) = 0
q(2) = min {q(1) + 1 , q(4) + 2}
q(3) = q(2) + 3
q(4) = q(3) - 5 |
|
Note that here we deliberately use q(j) rather than f(j) in the equation to highlight the distinction between the definition of f, namely (9), and the equation that it must satisfy, namely (11)-(13). Upon substituting q(1) = 0 and q(4) = q(3) - 5 in the expression for q(2), and then q(3) = q(2) + 3 in the resulting expression, we obtain q(2) = min {1,q(2)}. This equation has infinitely many solutions of the form q(2)=a, where a is any scalar not greater than 1. Thus, our functional equation has infinitely many solutions that can be characterized parametrically as follows:
| |
q(1) = 0
q(2) = a
q(3) = a + 3
q(4) = a - 2 |
|
(a <= 1) |
By inspection it follows that the length of the shortest path from node 1 to node 2 is equal to 1, hence f(2)=1. This means that in the case of the shortest path problem under consideration a=1 and therefore the solution of the functional equation corresponding to this problem is q(1)=0, q(2) = 1, q(3) = 4, q(4) = -1. Hence the lengths of the shortest paths are f(1)=0, f(2) = 1, f(3) = 4, and f(4) = -1.
Let us now solve this equation by successive approximation. At each iteration we shall solve the functional equation for j=1,2,3,4 - in this order. And to accelerate the performance of the procedure we use new values of {q(j)} as soon as they are computed rather than wait for the official termination of the current iteration.
Initialization: q(1)=q(2)=q(3)=q(4)=0.
Iteration # 1:
q(1) = 0
q(2) = min {q(1) + 1 , q(4) + 2} = min{1 , 2} = 1
q(3) = q(2) + 3 = 1 + 3 = 4
q(4) = q(3) - 5 = 4 - 5 = -1
Iteration # 2:
q(1) = 0
q(2) = min {q(1) + 1 , q(4) + 2} = min{1,1} = 1
q(3) = q(2) + 3 = 1 + 3 = 4
q(4) = q(3) - 5 = 4 - 5 = -1
Since there was no change in q we stop. The solution (fixed point) generated by this process is then q(1)=0, q(2)=1, q(3)=4, q(4)=-1.
Now, let us repeat the process, using a different initial approximation:
Initialization: q(1)=q(2)=q(3)=0, q(4)=-3.
Iteration # 1:
q(1) = 0
q(2) = min {q(1) + 1 , q(4) + 2} = min{1 , -1} = -1
q(3) = q(2) + 3 = -1 + 3 = 2
q(4) = q(3) - 5 = 2 - 5 = -3
Iteration # 2:
q(1) = 0
q(2) = min {q(1) + 1 , q(4) + 2} = min{1,-1} = -1
q(3) = q(2) + 3 = -1 + 3 = 2
q(4) = q(3) - 5 = 2 - 5 = -3
Since there was no change in q we stop. This time the solution (fixed point) generated by this process is q(1)=0, q(2)=-1, q(3)=2, q(4)=-3.
The question therefore arises: which one of these two solutions, if any, is the optimal solution to the shortest path problem under consideration? Recall that the equation under consideration actually has infinitely many solutions.
Because the problem under consideration is so small it is easy to resolve this ambiguity by inspection. But how do we resolve this matter in the context of large problems? In other words, how do we make sure that the solution generated by successive approximation yields a solution to the shortest path problem of interest?
We leave this as an exercise for the interested reader. Hint: think about an initial approximation that will resolve this dilemma.
And to show how important the initial approximation could be, let us reverse the order in which the {q(j)} values are updated:
Initialization: q(1)=q(2)=q(3)=q(4)=0.
Iteration # 1:
q(4) = q(3) - 5 = 0 - 5 = -5
q(3) = q(2) + 3 = 0 + 3 = 3
q(2) = min {q(1) + 1 , q(4) + 2} = min{1 , -3} = -3
q(1) = 0
Iteration # 2:
q(4) = q(3) - 5 = 3 - 5 = -2
q(3) = q(2) + 3 = -3 + 3 = 0
q(2) = min {q(1) + 1 , q(4) + 2} = min{1 , 0} = 0
q(1) = 0
Iteration # 3:
q(4) = q(3) - 5 = 0 - 5 = -5
q(3) = q(2) + 3 = 0 + 3 = 3
q(2) = min {q(1) + 1 , q(4) + 2} = min{1 , -3} = -3
q(1) = 0
This is a major disaster! The third iteration takes us back to exactly where we were at the end of the first iteration. This means that if we continue the process we shall enter into an infinite loop without ever reaching a fixed point.
One way to prevent this from happening is to use an initial approximation that guarantees that the sequence {q(m)(j): m=1,2,...} is non-increasing with m, that is q(m+1)(j) <= q(m)(j) for all j=1,2,...,n and m >= 0.
Exercise 13 Show that if the inter-city distances are nonnegative then the initial approximation q(0)(1)=0, q(0)(j)=infinity, j=2,...,n will always yield a fixed point for (11)-(13).
Hint:
(a) Show that the above initial approximation yields q(1)(j) <= q(0)(j) for j=1,2,...,n.
(b) Show, by induction on m, that this implies that q(m+1)(j) <= q(m)(j) for all j=1,2,...,n and m >=0.
The generic successive approximation method we outlined above deploys the equation it attempts to solve as a mechanism for updating the current approximation. That is, to solve x=g(x) it uses x(m+1) = g(x(m)) to update the current approximation for x. But sometime, to solve x =g(x) it might be better (eg more efficient) to use a different (but obviously related) equation or recipe to update x. In particular, in the case of the dynamic programming functional equation (11)-(13) it might be more efficient computationally to use Push (20) rather than Pull (18) as the updating mechanism. By the same token, since in the context of (11)-(13) the object being approximated {f(j)} is multi dimensional, the question arises: in what order the components of this object should be updated?
Thus, in practice it is useful to make the format of the generic successive approximation method more flexible. First, we can distinguish between the equation we wish to solve, x=g(x), and the updating recipe, say x = G(x). Second, it is useful to let G incorporate an exogenous parameter so instead of x = G(x) we write x = G(x;p) where p denotes a parameter used in the updating of x. It is assumed that the parameter itself is updated by the rule p = H(p;x). To initialize the procedure we thus need an initial approximation for x and an initial value for p.
As we have shown in Appendix A, Dijkstra's Algorithm is a successive approximation method characterized by the following three features:
- A simple initial approximation: F(1)=0, F(j)=infinity, j=2,...,n.
- A Push-type updating mechanism, (14).
- A Best-first processing order, (15).
The algorithm has the nice property that even in the presence of cycles, if the distances are not negative then there are at most n updates before a fixed point of (11) is reached. Furthermore, in each update at least one new F(j) value attains it exact final value (f(j)) and is not affected by subsequent updates.
Exercise 14
Formulate Version 1 of Dijkstra's Algorithm as a successive approximation method of the form x = G(x;p), p = H(p;x).
Hint: Let x represent F and p represent U, and define G and H accordingly. Thus, in this framework G represents the Push operation and the "greedy" selection rule (15), and H represents the dynamics of U.













